Round Wire ac Resistance Calculator

Calculates the ac resistance of a round straight wire for common conducting materials using the equation and data referenced below or by manually entered material data.

  Note: To use different values for the Resistivity and Relative Permeability, select Enter Data in the Conductor Material selection text box and then enter the relevant values in the boxes highlighted in amber.

This calculator uses JavaScript and will function in most modern browsers. For more information see About our calculators

  The a.c. resistance for the length of round straight wire is calculated using the conductor resistivity, the length of the conductor and the effective cross sectional area used by the skin effect.

  The cross sectional area used by the skin effect is found by first calculating the nominal depth of penetration for a conductor.

  From Transmission Lines and Networks by Walter C. Johnson, McGraw-Hill 1963 p58.

The values for μ_r are from Transmission Line Design Handbook by Brian C Wadell, Artech House 1991 Table 9.3.2 page 446.

The values for ρ are from CRC Handbook of Chemistry and Physics 1st Student Edition 1998 page F-88 and are for high purity elements at 20°C.

  The actual cross sectional area used due to skin effect can be calculated by several methods with varying degrees of accuracy. The simplest method is to multiply the skin depth by the circumference of the conductor.

Where d is the diameter of the conductor

  This method makes the used cross sectional area too large from high frequencies down to the point where skin depth becomes about half of the radius of the conductor, at which point the inaccuracies increase and eventually the calculated used area becomes bigger than the actual conductor. Making the calculation method only an approximation and then only usable when r >> δ.

  A second simple method is to calculate the total area of the conductor and then subtract the area of a circle that represents the central area that does not use skin effect.

Where r is the radius of the conductor

  This method is more accurate the first method when r >> δ but becomes highly inaccurate below the point where d/δ = π and can have huge positive or negative swings in value.

  A much more accurate method is described by David Knight in a very detailed article entitled Zint.pdf which can be found in http://www.g3ynh.info/zdocs/comps/part_1.html This method uses a truncated exponential decay method to remove the errors caused when the actual conductor area becomes less that the calculated skin depth area in the simple method above, and a modified Lorentzian correction which removes the error that occurs as the calculated skin depth area approaches the actual conductor area. The author refers to this equation as Rac - TED - ML and quotes a maximum error of 0.09%.

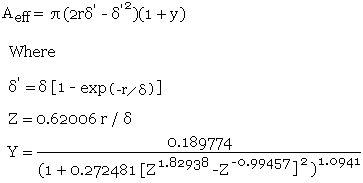
  The calculation method assumes that there is a single isolated conductor and takes no account of a return path. This makes it rather difficult to measure end to end and so the results of this calculator have been compared with figures given in the original article in order to prove accuracy.

W J Highton 30/9/2011

This calculator is provided free by Chemandy Electronics in order to promote the FLEXI-BOX

Return to Calculator Index