Impedance of a Round Straight Wire Calculator

Calculates the impedance of a round straight wire for common conducting materials using the formula and data referenced below or by manually entered material data.

The real part of the impedance (a.c. resistance) for the length of round straight wire is calculated using the conductor resistivity, the length of the conductor and the effective cross sectional area used by the skin effect.

Where ρ is the resistivity of the conductor in Ω.m

l is the Length of the conductor in mm

A_eff is the effective cross sectional area used in mm

The cross sectional area used by the skin effect is found by first calculating the nominal depth of penetration for a conductor.

From Transmission Lines and Networks by Walter C. Johnson, McGraw-Hill 1963 p58.

Where ρ is the resistivity of the conductor in Ω.m

f is the frequency in Hertz

μ is the absolute magnetic permeability of the conductor

The absolute magnetic permeability (μ) = μo x μr

μo = 4π x 10^-7 H/m

The values for μr are from Transmission Line Design Handbook by Brian C Wadell, Artech House 1991 Table 9.3.2 page 446.

The values for ρ are from CRC Handbook of Chemistry and Physics 1st Student Edition 1998 page F-88 and are for high purity elements at 20°C.

The effective area is then found using a formula by David Knight and this comes from a very detailed article entitled Zint.pdf which can be found in http://www.g3ynh.info/zdocs/comps/part_1.html and is well worth a read! This formula uses a truncated exponential decay method to remove the errors caused when the actual conductor area becomes less that the calculated skin depth area in the simple method above, and a modified Lorentzian correction which removes the error that occurs as the calculated skin depth area approaches the actual conductor area. The author refers to this formula as Rac - TED - ML and quotes a maximum error of 0.09%.

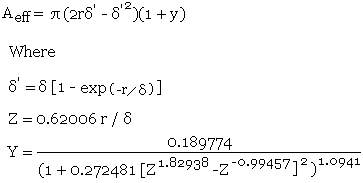
and r is the radius of the conductor

The resistance is then calculated from the formula shown above.

The imaginary part of the impedance (reactance) for the wire is calculated from the sum  of the internal inductance and the external inductance. The internal inductance is calculated first using another formula from Zint.pf referred to as Li - ACA3.74ML.

The external inductance is then calculated using a formula from Rosa which can be found near the top of part_2 of the above article.

The total inductance is then found by adding the internal inductance and the external inductance.

L = Li + Le

The reactance of the total inductance can then found using:-

X_L = 2πfL 

The calculation method assumes that there is a single isolated conductor and takes no account of a return path. 

W J Highton 4/10/2011

This calculator is provided free by Chemandy Electronics in order to promote the FLEXI-BOX

Return to Calculator Index